I numeri immaginari apparvero in matematica per la prima volta quando nel Cinquecento vennero scoperte le formule per risolvere le equazioni di terzo e quarto grado.
Queste formule, in alcuni casi, richiedevano di estrarre radici quadrate di numeri negativi.
A noi al liceo ci hanno insegnato che i numeri immaginari appaiono nelle possibili soluzioni delle equazioni di secondo grado del tipo:
ax2 + bx +c = 0

quando Δ = b2 – 4ac < 0
che da soluzioni immaginarie. Infatti si dovrebbe estrarre la radice quadrata di un numero negativo. Ma nella risoluzione dei nostri problemi, noi ci limitavamo a dire che la equazione non dava soluzioni per Δ<0, o che la equazione dava due soluzioni non reali, immaginarie per l’appunto, e poco ci interessava del resto.
Poi scopri che bastava dare una occhiata alla equazione (x2 + 1 = 0) ovvero (x2 = – 1) per capire che nessun numero elevato al quadrato mi dava -1, che non era possibile estrarre la radice quadrata di -1.

E così si è pensato di sistemare le cose introducendo una lettera, un operatore, una unità immaginaria pari alla radice quadrata di -1.
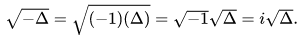
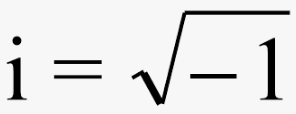

Per cui x = i.
Es:
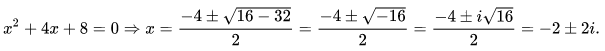
Per la rappresentazione grafica di questo risultato è stato necessario ipotizzare un piano con asse (x) per valori reali e un asse (y) per i numeri immaginati.
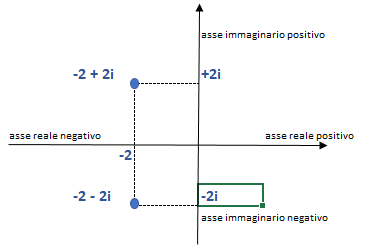
Alla domanda a cosa servono i numeri immaginari, la prima risposta è che rendono possibili la soluzione di equazioni altrimenti impossibili e che possono essere inseriti nelle operazioni con i numeri reali sotto forma di numeri complessi (a + ib) con (a) e (b) numeri reali.
Es:
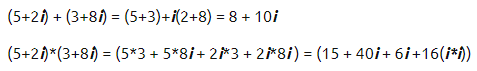
A questo punto la seconda domanda è cosa rappresenta quella parte immaginaria, a cosa serve.
La fisica dei numeri complessi
In fisica i numeri complessi vengono utilizzati ad esempio per descrivere i fenomeni ondulatori; inoltre, l’unità immaginaria appare esplicitamente nella celebre equazione di Schrödinger, che descrive l’evoluzione di un sistema fisico nell’ambito della meccanica quantistica.
Sono anche utilizzati in fluidodinamica per descrivere il flusso potenziale in due dimensioni, nella teoria della relatività, dove alcune formule dello spazio metrico diventano più semplici con il loro impiego, in ingegneria elettrotecnica.
Moto armonico
Si definisce, molto banalmente, moto armonico il moto di un punto lungo una retta che va avanti e indietro oscillando tra due posizioni.

Questo moto se ci pensiamo un attimo può essere assimilato alla proiezione di un punto P sull’asse delle ascisse che si nuove lungo una circonferenza di raggio unitario.
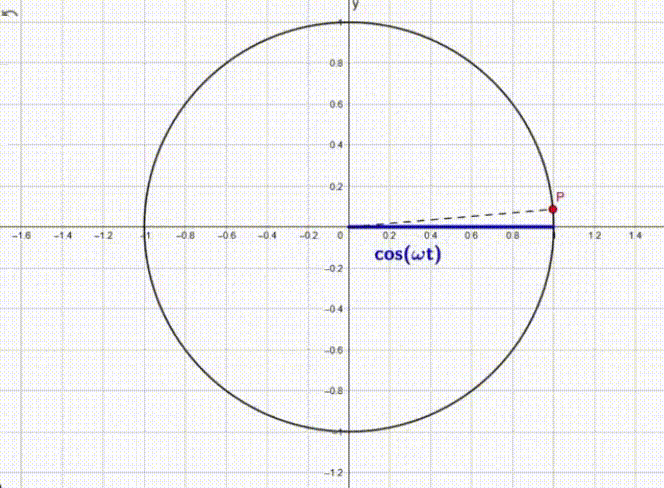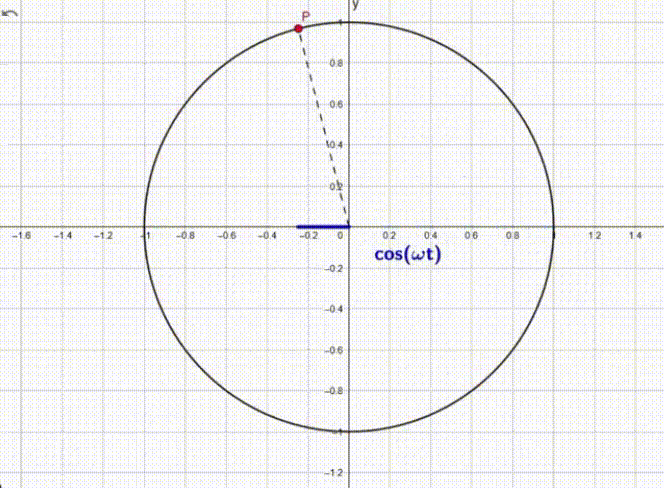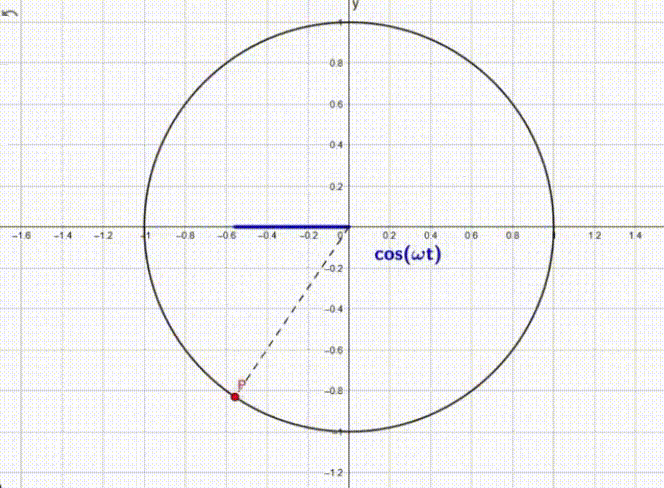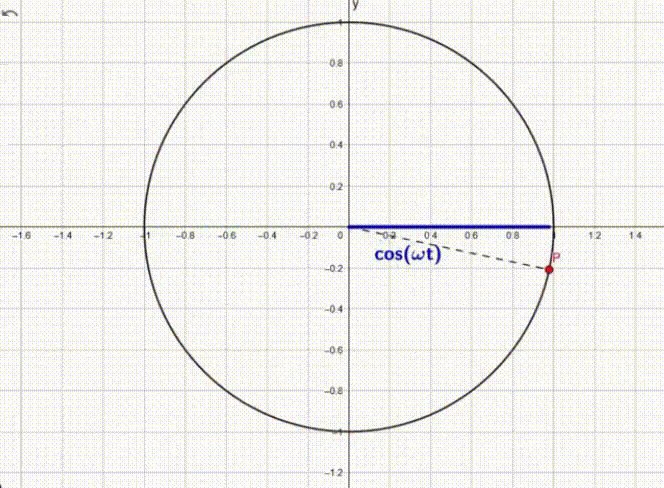
Come si può vedere la proiezione del punto sull’asse x va avanti e indietro come un moto armonico.
In trigonometria questo andamento è il valore dato dal raggio (in questo caso =1) moltiplicato il coseno dell’angolo che forma con l’asse (x).

cos(α) = cos(ωt)
Dove α è l’angolo sotteso, ω è la velocità angolare del punto sulla circonferenza e ωt rappresenta il suo spostamento.
Alla stessa maniera il nostro punto proietta la sua immagine anche sull’asse y che ha lo stesso moto armonico sull’asse x e dato dal valore trigonometrico:
sin(α) = sin(ωt)
Questo asse (y) che esiste di fatto solo sul faglio di carta, non in realtà, viene chiamato asse immaginario. Quindi il nostro punto può essere così rappresentato su un piano complesso chiamato piano di Gauss.
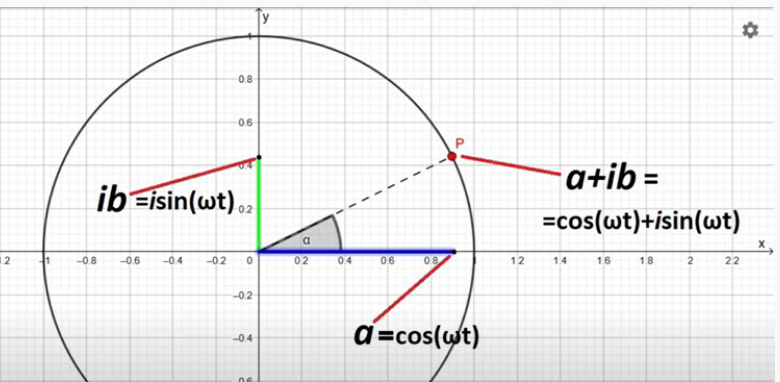
P = a + ib = cos(ωt) + i sin(ωt)
dove (P) è il numero complesso, (i) la unità immaginaria, (b) la parte immaginaria
Equazione di Schrödinger
Nella fisica atomica l’equazione di Schrödinger è una formula per descrivere la posizione e il moto degli elettroni intorno al nucleo, tramite una funzione d’onda.


Cos’è l’operatore hamiltoniano? Per i più pignoli l’operatore hamiltoniano 

 ,
,  .
.
Circuito RLC

Il circuito RLC contiene solo resistori (R), induttori (L) e condensatori (C) e costituisce un oscillatore armonico. L’oscillatore armonico è un sistema meccanico che reagisce ad una perturbazione dell’equilibrio con una accelerazione di richiamo proporzionale allo spostamento subito , esattamente come abbiamo visto precedentemente.
Se identifichiamo il piano (x, y) col piano di Gauss dei numeri complessi z = x+iy,
allora il vettore V (t) si può interpretare come numero complesso:
V (t) = V0 (cos ω t + i sinωt)
Più precisamente

dove X è la Reattanza e Z la impedenza del circuito
O più semplicemente V = R +jXI = ZI
Le seguenti figure illustrano le “oscillazioni” della tensione (V) e della corrente (I) nel piano complesso nei vari componenti del circuito.

Cationi
Quando si viaggia a grandi velocità si entra nel campo della relatività ristretta. Alla formula di Einstein E=mc2 viene aggiunto il fattore di Lorenz diventando

Dove (m) è la massa, (v) la sua velocità, (c) la velocità della luce.
La massa ‘m’ è legata alla massa a riposo m0 tramite il fattore di Lorenz e viene chiamata massa relativista.

Dal momento che è una semplice espressione matematica nulla mi vieta di considerare v>c.
v2/c2 >1, diventa maggiore di uno e il denominatore diventa la radice quadrata di un numero negativo (numero immaginario),
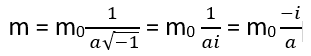
Nel momento in cui la massa raggiunge la velocità delle luce diventa improvvisamente immaginaria facendo comparire le famose particelle “virtuali” chiamate tachioni, di massa immaginaria per l’appunto.
Appendice
Complesso coniugato e reciproco di un numero complesso
Il complesso coniugato del numero complesso 
Conoscendo il valore assoluto e il coniugato di un numero complesso 

Ossia, se 
L’equivalente della formula riportata in intestazione del post.
L’inverso di un numero a è un numero b tale che a*b=1. L’inverso di a si indica solitamente come a-1. Con le frazioni invece b=1/a. Pertanto l’inverso di 3 è 1/3, l’inverso di -3 è –(1/3)… e la regola vale anche per le frazioni: l’inverso di 1/3 è 1/(1/3)=3.

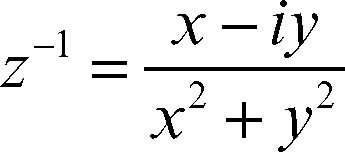

 , esattamente come abbiamo visto precedentemente.
, esattamente come abbiamo visto precedentemente.


